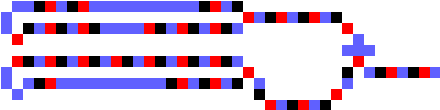
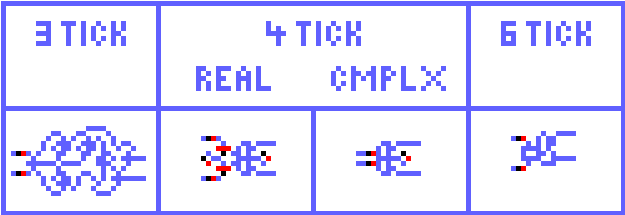
The Minuscule 3-tick Latch
In January of 1990 when A. K. Dewdney's article appeared in SA I saw how to do 4-tick logic, but not 3-tick. The few 3-tick gates I came up with were clumsy. And I didn't have a latch. So I developed my Complex, 4-tick methodology. In February 1990 I went to sleep for about 14 years.
After tripping over some WireWorld work on the internet in late 2003 I took up my 4-tick work, making a binary multiplier and Turing Machine, among other things. In late 2004 Karl Scherer and I did a little work in 3-tick and those gates were given on this web site until now.
Luckily I also ran into Michael Greene recently. Michael's work in 3-tick WireWorld is amazing. This gentleman has a very devious mind. One or two of the 3-tick gates are smaller than any other tick, and many are about the size. A few are large, such as the XOR and cross.
My guess is that the area required for the random logic of a device could be about the same or could be a lot larger for 3-tick than 4-tick or 6-tick, depending upon the specific design. For example, a machine with a lot of XORs would be larger in 3-tick than higher ticks. As is the case for the Full Adder. A machine with a lot of crosses would also be larger in 3-tick. But in the absence of XORs and crosses, 3-tick may even be the smallest.
The space required for long data loops, however, is always less for 3-tick. So a very large binary multiplier, say 16 bytes by 16 bytes, would be take about 3/4 the space of a 4-tick version. And run faster to boot.
I am going to break from my normal guideline of only presenting devices that I designed myself. With the permission of Michael I am giving his ANDNOT, NOT, RS Latch, T Latch, XOR, and Cross. The only 3-tick device of mine that's worth keeping is my 'minuscule' RS Latch.
And since it's my web page, I get to go first.
This latch is exactly the same as the previously-invented 4-tick version. It has negative level Set and Reset inputs. The output is also negative level. It is essentially an ANDNOT gate with the -Set being the allowing leg and the -Reset being the inhibiting leg. It is set dominant.
The latch can also be viewed as a reset-dominant latch with positive level output. This is done by making the -Set the inhibiting leg and the -Reset the allowing leg. The latch works perfectly as the carry latch in the binary multiplier.
It is quite astonishing to me that such a small device exists. And that you can make a latch without a loop.

All the 3-tick gates presented in this section are Michael Greene's inventions.
I'm also giving the 4-tick and 6-tick versions of these gates. The 4-tick is given for both Real and Complex input, but only Real output (except the OR).
You can download the whole smash of gates in MCell
Source Code.
The OR gate works at any speed. The Complex-input 4-tick OR gate is slightly simpler. Don't laugh, this actually saved me a little space once.
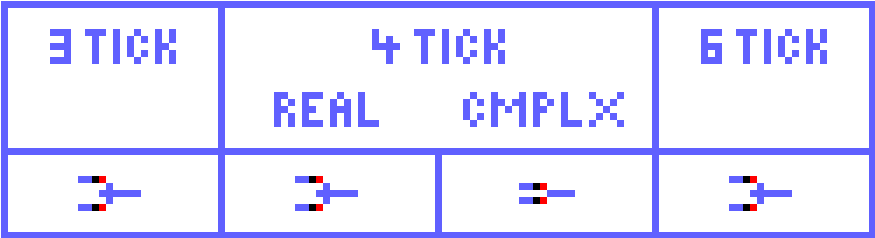
The Complex 4-tick and 6-tick ANDNOTs work for any sequence of inputs. This is not true for the 3-tick and Real 4-tick versions. The simpler configuration on the top works as long as the previous output was off, the present inhibiting leg is off, or the present allowing leg is off.
If I had been paying attention, this device could have been used in the full adder in my 4-tick binary multipliers. It eventually dawned on me that they are actually latches.
The bottom two gates work for any combination of inputs.
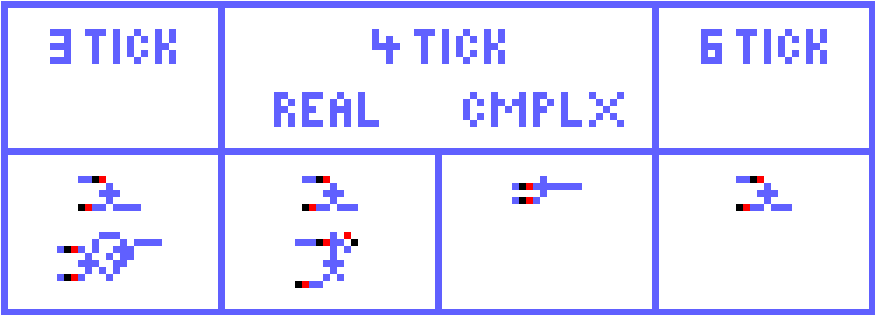
This is the first 3-tick device Michael showed me. I was nonplussed. Two version of each are given. Notice the 3-tick methodology used in the second 4-tick and the 4-tick methodology in the 6-tick.
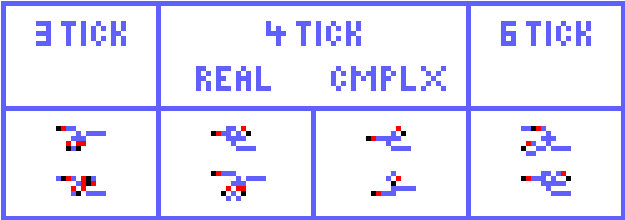
The top four latches are positive-input, positive-output, reset-dominant. Of course, switching the sense of set and reset makes them positive-input, negative-output, set-dominant.
The bottom two latches are my aforementioned 'minuscule' latches. They are negative-input, positive-output, reset-dominant, or negative-input, negative-output, set-dominant.
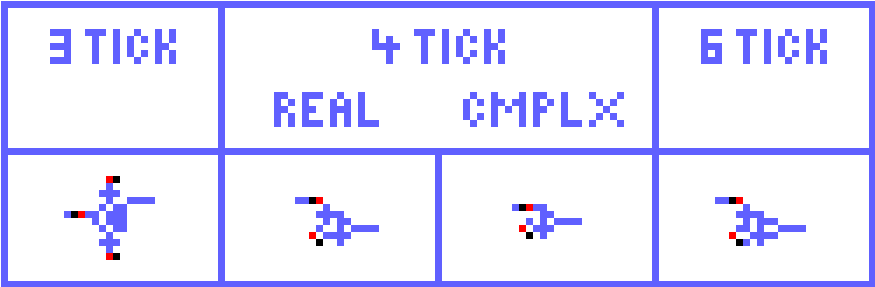
Another of Michael's marvels. It features a center 2-by-4 block of frequency 3 that changes state with an input pulse. And the diodes top and bottom to keep reverse traveling electrons from the system.
The 4-tick design is again mine. Perhaps a minor marvel. I think this method also produces the nicest 6-tick latch available.
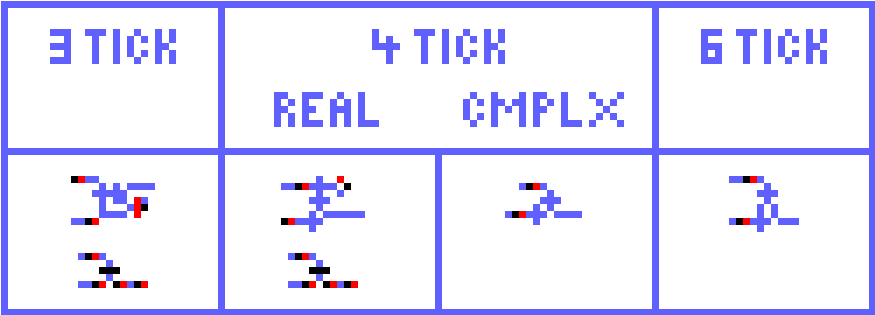
This is one of the places that 3-tick costs more. Maybe Michael will find a minute XOR soon.
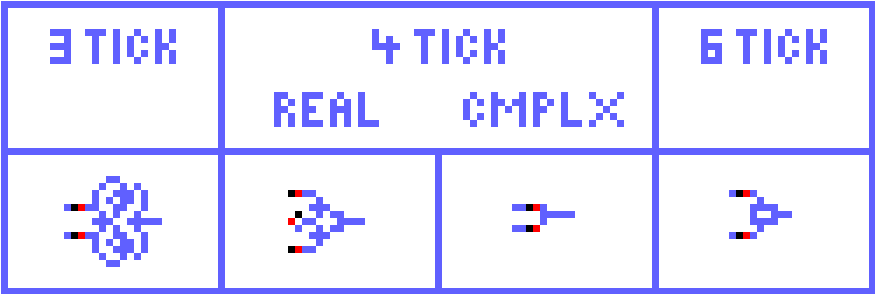
Here again 3-tick is not very economical.
But too much is made of the size of crosses. I'm not that concerned. There always seems to be a way to do without them. I have actually never used a full cross in any design. Mark Owen's computer does have one though.
The 6-tick cross is also Michael's design. And the 4-ticks are my layouts, using Michael method.
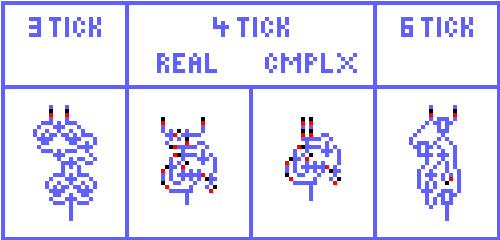
Each of these full adders works about the same. XOR the inputs. Fiddle with this a little to get Set and Reset to the carry latch. The sum is the XOR of the carry with the previous XOR.
I used a 'minuscule' RS Latch in the 3-tick version. Otherwise it's just two of Michael's XORs and an OR gate. I'd bet this can be done more efficiently . The 4-tick is a redesign of the full adder in my binary multiplier. It also used two XORs, and OR, and a RS latch, this time just a normal latch. Internal Complex logic is used. The 6-tick was taken from the computer design.
I used the previous full adder in the 3-tick multiplier. The gate is made up of a latch, a full ANDNOT, and a couple of 6-tick-type ANDNOTs. The clock uses the fact that 189 = 7 * 27.
A couple of interesting observations about the 3-tick FA. First, there are no eletrons present when in its quiescent state. The 4-tick has internal Complex gates, so will always have eletrons. Even the 6-tick has an inverter, so always an electron. Second, the 3-tick FA can run a 4-tick speed by increasing the path to the reset of the RS latch by one cell. Nifty.
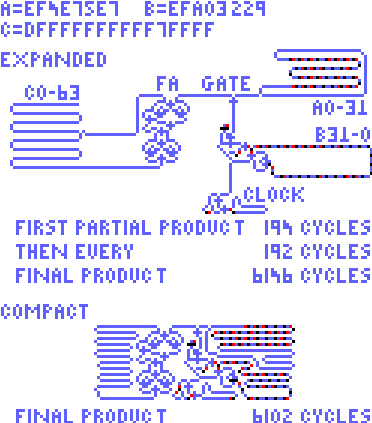
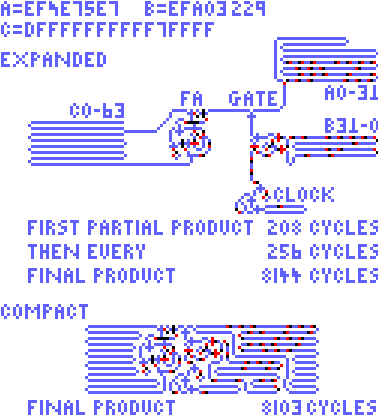
This is an updated version of the 4-tick binary multiplier. It removes some redundant logic and uses better gates and simpler random logic. The random logic in the FA and Gate is less than that of the 3-tick multiplier. The clock is slightly larger. And the loops are 33% longer.